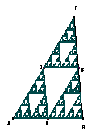Geometrix: Interaktive Geometrie

Software zum Experimentieren mit/Konstruieren von Objekten der Euklidischen Geometrie wie Dreiecke, Vierecke, Winkel, Kreise, Punkte, Parallelen.

• Mittels Punkten, Geraden, Strahlen, Kreisen können Figuren konstruiert werden.
• Örter, Flächeninhalte, Winkel, Längen können gemessen werden.
• Über affine Abbildung (oder "Ersetzung von Dreiecken") auch Erstellung von Fraktalen.

Ideal geeignet für den experimentellen Unterricht in Geometrie.

Deutsche Version Euro 20

(Klassenraumlizenz für Euro 80, Schullizenz Euro 200)

Bestellen Sie mit dem Bestellformular!

Auszug aus der Kurzanleitung:

Einführung Geometrix ist ein Windows-Programm für "2D-Geometrie" mit dem Computer für Schüler ab ca. 11 Jahre. Die dänische Urfassung stammt von Prof. Viggo Sadolin von The Royal Danish School Of Educatio-nal Studies; die deutsche Version wird exklusiv vertrieben von mathemas. Geometrix wurde als Zeichen-, Berechnungs- und Konstruktionsprogramm für den Unterricht konzipiert. Geometrix ist menügesteuert, aber die meisten Operationen können mit der Maus durchgeführt werden. Mit dem Programm können geometrische Figuren (Punkte, Geraden, Strahlen, Kreise und daraus abgeleitete) gezeichnet werden und auf vorhandenen Objekten basierende neue Objekte (z. B. Dreiecke, Winkel, ja sogar Fraktale) konstruiert werden.

Es kann mit oder ohne sichtbarem Koordinatensystem gearbeitet werden. In einem Eingabefeld können Koordinaten von Punkten und Geradengleichungen angegeben werden. Bei Änderung bleiben Eigenschaften, wie Mittelpunkt, Mittelsenkrechte, Winkelhalbierende erhalten. Mit der Maus können Punkte etc. bewegt und dabei kann die Änderung von Figuren betrachtet werden. Über Menüpunkte können Abstände, Winkel und Flä-chen berechnet werden.

Der Umgang mit dem Programm ist recht schnell und durch Ausprobieren zu erlernen; der Einsatz in Schulen hat gezeigt, dass sogar 11-jährige es nach ca. 30 Minuten schaffen.

Didaktischer Hintergrund

Was man mit dem Unterrichts-Tool Geometrix machen kann, beschreibt Viggo Sadolin in der zusätzlichen Dokumentation "Exploring Geometry using Geometricks".

Im Vorwort liest man, dass Geometrie in der Schule nicht nur eine Welt der Zeichnungen und Berechnungen alleine bleiben soll, Schüler sollten vielmehr in eine mehr theoretische Welt eingeführt werden, die aus Sätzen und Beweisen, Behauptungen und Begründungen be-steht. Dies sei nicht einfach zu erreichen in der Schule.

Wenn wir beweisen, argumentieren und begründen sagen, meinen wir die Arbeit an einer allgemeinen Wissensgrundlage in der Geometrie. Was ist ein Beweis? Wie tief sollte man argumentieren, ehe man etwas als Beweis akzeptiert? Es ist notwendig, eine gemeinsame Wissensgrundlage zu schaffen, auf der Begründungen aufbauen können. Es ist wahrscheinlich keine gute Idee, in den Grundkursen axiomatische Geometrie einzuführen. Als Lehrer muss man sich darauf einrichten, auf einer etwas unsicheren Grundlage zu arbeiten.

Bestellen Sie mit dem Bestellformular!

Fraktale mit Geometrix

Auszug aus der Anleitung:

Diese Anleitung ist eigentlich nicht für Schüler geschrieben, sondern wurde geschrieben für Lehrer oder fortgeschrittenen Leser, die wissen, was z.B. affine Abbildungen und/oder Fraktale sind. Geometrix erzeugt Fraktale mittels affiner Abbildungen der Ebene. Das Grundprinzip soll hier erläutert werden, dabei wird auch eine anschaulichere alternative Sicht der Prozedur angeboten. Praktische detaillierte Übungen sollen die Einarbeitung erleichtern.

Affine Abbildung Zuerst einmal soll der Begriff der affinen Abbildung, so wie er hier benutzt wird, eingeführt werden. Ausgehend von drei Punkten in der Ebenen, die nicht alle auf einer Geraden liegen (Nichtkollinearität), die also ein echtes Dreieck bilden, läss t sich ein, wenn auch schiefwinkliges Koordinatensystem konstruieren. Diese drei Punkte seien A, B, C (siehe Abbildung 1). Mit dem Punkttripel (A, B, C) wird auch das entsprechende Dreieck bezeichnet. Nun nehme man A, den ersten der drei Punkte, als Ursprung. Der Vektor von A nach B sei dann der Basisvektor für die erste Dimension, der Vektor von A nach C der für die zweite Dimension. Dieses so definierte Koordinatensystem sei dann Ko[A, B, C]. Jeder Vektor mit Ursprung in A läss t sich als Linearkombination der beiden Basisvektoren schreiben; die Koeffizienten der Linearkombination sind dann die Koordinaten des Endpunktes des Vektors.

Abbildung 1

Es sei nun f eine Abbildung in der Ebene; f heißt affine Abbildung, wenn es ein wie oben beschriebenes Dreieck gibt, also Punkttripel (A, B, C) und wenn die Koordinaten eines Punktes P bezüglich des Koordinatensystem Ko[A, B, C] die gleichen sind wie die von f(P) im Koordinatensystem Ko[D, E, F], wobei D=f(A), E=f(B), F=f(C).

Umgekehrt definieren zwei vorgegebene Punkttripel (nichtkollinear) eine affine Abbildung, und man kann dann etwas lax schreiben

f=[Ko[A,B, C], Ko[D, E, F]].

Eine wichtige Beobachtung: Wird die Dreiecksfläche ABC mit M bezeichnet, so wird f(M) zur Fläche des Dreiecks DEF. Im folgenden werden die Bilder der Menge M betrachtet.

Durch entsprechende Wahl der Dreiecke lassen sich bekannte affine Abbildungen definieren:

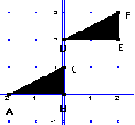
Translation (man nehme zum Beispiel A, B, C, D, E, F wie in Abbildung 2)	Abbildung 2
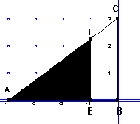
Streckung (A, B, C, D=A, E, F wie in Abbildung 3)	Abbildung 3
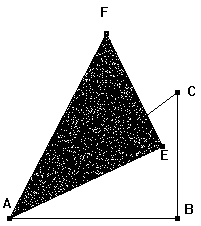
Drehung (siehe Abbildung 4)	Abbildung 4

Kombinationen oder Hintereinanderausführungen dieser affinen Abbildungen sind, wie man sich überlegen kann, auch wieder affine Abbildungen.

Sierpinskis Dreieck

Dies ist vielleicht das bekannteste durch affine Abbildungen definierte Fraktal und soll zur Erläuterung und Weiterführung dienen.

Man beginnt mit einem großen Dreieck ABC, konstruiert die Mittelpunkte der Dreiecksseiten, benennt sie entsprechend D, E, F.

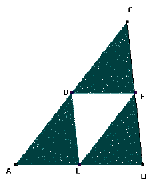
Abbildung 5

Durch die so gebildeten 4 Dreiecke erhält man 3 affine Abbildungen. f=[Ko[A,B, C], Ko[A, E, D] ]-- Streckung mit Faktor 1/2 g=[Ko[A,B, C], Ko[E, B, F] ]-- Streckung mit Faktor 1/2 gefolgt von Translation h=[Ko[A,B, C], Ko[D, F, C] ]-- Streckung mit Faktor 1/2 gefolgt von Translation Füllt man nun f(M), g(M), h(M) aus, so ergibt sich Abbildung 5; in Geometrix heißt es das Schritt 1 Bild.

Im Schritt 2 werden alle möglichen Produkte mit zwei Faktoren der Abbildungen f, g, h betrachtet.

Die Bilder der Menge M f(f(M)), f(g(M)), g(f(M)), g(g((M)), f(h(M)), h(f(M)), ... ergeben das "Schritt 2 Bild".

Ein weiteres Beispiel

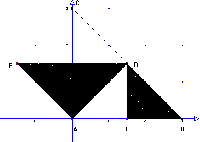
Abbildung 8

Man wähle die drei Punkttripel (A, B, C), (A, D, E), (F, B, D) wie in Abbildung 1. Die Dreiecke definieren zwei Abbildungen f=[Ko[A,B, C], Ko[A, E, D] ] und g=[Ko[A, B, C], Ko[F, B, D]]. Dann ergibt sich das Schritt 1 Bild (siehe Abb. 8) Man kann die Konstruktion mit den Abbildungen auch etwas anschaulicher beschreiben: Im ersten Schritt wird das Dreieck (A, B, C) durch die beiden Dreiecke (A, D, E), (F, B, D) ersetzt, im zweiten Schritt die beiden Dreiecke (A, D, E), (F, B, D) dann jeweils durch entsprechende Dreiecke.

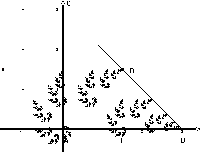
Abbildung 9

Nach sehr (eigentlich unendlich) vielen Schritten ergibt sich dann die Fraktale (siehe Abbildung 9). Die Erläuterung der Prozedur als "Ersetzung von Dreiecken" ist wahrscheinlich sehr viel anschaulicher und führt auch zum Abbildungsbegriff. Es wird dann auch einfacher zu überlegen, wie man andere Fraktale erzeugen könnte (zum Beispiel: Könnte man Vierecke statt Dreiecke verwenden? Welchen Körper könnte man im 3D für die Erzeugung räumlicher Fraktale verwenden?) usw.